Data briefing

Kaggle supplies five data sets for the competition, three of which can be used in model training. The train.csv file includes several variables associated with each West Nile Virus test including the trap id, geo-coordinates, date, species of mosquito present, number of mosquitoes present, and a binary variable indicating the presence or absence of West Nile Virus (WnvPresent), our target variable. The test.csv contains all the same features as the train.csv file except the number of mosquitoes present and the target WnvPresent variable. These data sets were obtained from West Nile Virus testing period between 2007 and 2014 with the training set containing the odd years and the test set containing the even years. The weather.csv file contains historic weather data collected at the O’Hare and Midway airports concurrent with the mosquito testing period. The spray.csv file includes the date and location of chemical spraying conducted by the city during 2011 and 2013. Since this spray data set would only have a large impact during one of the training years, I did not include the spray data in any of my models. For the weather data, since the differences in variables between O’Hare and Midway were generally small, I chose to use only the O’Hare data for all traps, rather than compute the closest station for each trap.

A large hypothetical variable influencing viral infection is population size. A larger population means there are more mosquitoes who can become infected, but it also increases the number of interactions between hosts, allowing faster spread of virus from individual to individual. The size of the population can be estimated from the number of mosquitoes found in each trap. However, this variable is not present in the test set, and will need to be imputed from other variables before a final model can be fit to the presence of West Nile using population as an input.

library(plyr)
library(tidyverse)

## Warning: Installed Rcpp (0.12.12) different from Rcpp used to build dplyr (0.12.11).
## Please reinstall dplyr to avoid random crashes or undefined behavior.

## Loading tidyverse: ggplot2
## Loading tidyverse: tibble
## Loading tidyverse: tidyr
## Loading tidyverse: readr
## Loading tidyverse: purrr
## Loading tidyverse: dplyr

## Conflicts with tidy packages ----------------------------------------------

## arrange():   dplyr, plyr
## compact():   purrr, plyr
## count():     dplyr, plyr
## failwith():  dplyr, plyr
## filter():    dplyr, stats
## id():        dplyr, plyr
## lag():       dplyr, stats
## mutate():    dplyr, plyr
## rename():    dplyr, plyr
## summarise(): dplyr, plyr
## summarize(): dplyr, plyr

load("west-nile/train.RData")
load("west-nile/test.RData")

ggplot(train, aes(x=WnvPresent, y=NumMosquitos)) + 
  geom_jitter(aes(color=WnvPresent)) + 
  ggtitle("Number of mosquitoes in West Nile \nVirus negative and positive traps") + 
  xlab("West Nile Virus present in trap") + ylab("Number of mosquitoes in trap")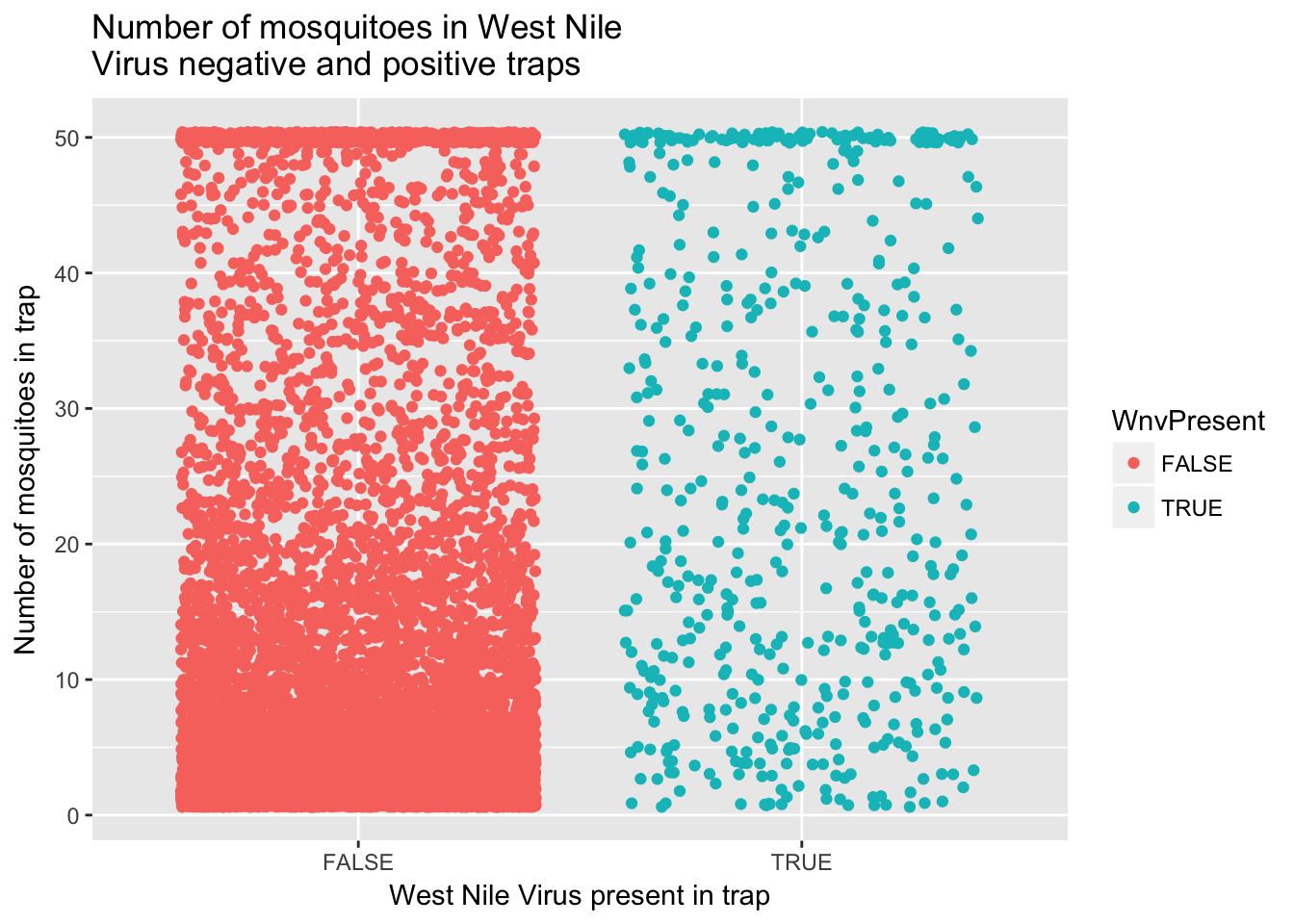

Based on this initial data exploration, I will first try and develop a model that predicts the number of mosquitoes in each trap and then use that predicted value as a variable in a model for WNV presence. For predicting the number of mosquitoes, I will first attempt using weather variables and weekly historic averages. Before modeling, I examined scatterplots of various input variables against mosquito counts, like the graph below comparing temperature to mosquito counts.

ggplot(train, aes(x=Tavg, y=Mosq_count)) + 
  geom_jitter() + 
  geom_smooth(method = lm) + 
  ggtitle("Number of mosquitoes vs average daily temperature") + 
  xlab("Average daily temperature, degree F") + ylab("Number of mosquitoes per trap")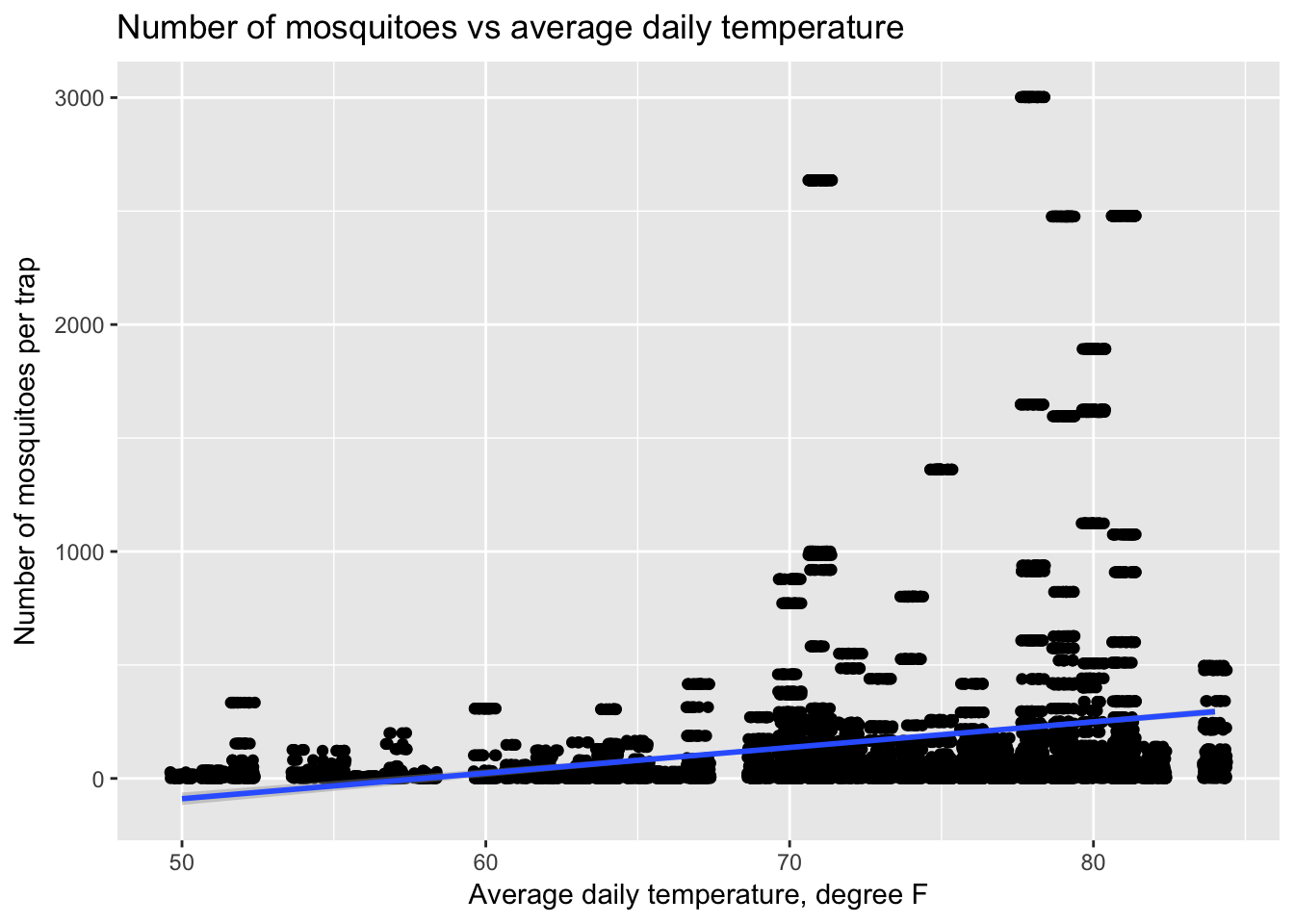

Tidying and transforming data

I cleaned up the weather and training data sets to impute missing values and delete non-informative columns. I next engineered several attributes from existing variables that I thought would be useful. Moving averages of temperature and precipitation, as well as weekly averages in overall mosquito counts were added to weather and training respectively. The code for variable engineering scripts (01_weather.R, 02_train_test.R) can be found in the src folder in the GitHub repo.

Modeling: Linear regression to predict mosquito population

For this first round of modeling, I will use linear regression to predict the number of mosquitoes using weather data and historical averages per week. I expect that higher average temperatures and greater moisture should have a positive effect on the mosquito population.

library(caret)

## Loading required package: lattice

## 
## Attaching package: 'caret'

## The following object is masked from 'package:purrr':
## 
##     lift

set.seed(123)
split <- createDataPartition(y = train$NumMosquitos, p = 0.75, list = FALSE)
number_train <- train[split,]
number_valid <- train[-split,]

lm_variables <- c("Tmax", 
                  "Tmin",
                  "Tavg",
                  "DewPoint",
                  "WetBulb",
                  "Sunrise",
                  "Sunset",
                  "PrecipTotal",
                  "ResultSpeed",
                  "ma3",
                  "ma5",
                  "ma10",
                  "precip3d",
                  "precip5d",
                  "precip10d")

lm_variables <- paste(lm_variables, collapse = "+")
fmla <- as.formula(paste("NumMosquitos", lm_variables, sep = "~"))


lm1 <- train(form = fmla, 
             data = number_train, 
             method = "lm")

number_train$lmNumMosq <- predict(lm1, newdata = number_train)
number_valid$lmNumMosq <- predict(lm1, newdata = number_valid)

train$lmNumMosq <- predict(lm1, newdata = train)
test$lmNumMosq <- predict(lm1, newdata = test)

summary(lm1)

## 
## Call:
## lm(formula = .outcome ~ ., data = dat)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -43.994 -10.576  -5.249   4.424  48.984 
## 
## Coefficients:
##               Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -211.35042   28.81977  -7.334 2.46e-13 ***
## Tmax           1.52788    0.39822   3.837 0.000126 ***
## Tmin           1.96311    0.39673   4.948 7.65e-07 ***
## Tavg          -3.66666    0.78568  -4.667 3.11e-06 ***
## DewPoint      -0.81267    0.13950  -5.826 5.92e-09 ***
## WetBulb        1.10331    0.21191   5.207 1.97e-07 ***
## Sunrise        0.09426    0.01627   5.792 7.22e-09 ***
## Sunset         0.06936    0.01210   5.733 1.02e-08 ***
## PrecipTotal   -0.46272    0.45810  -1.010 0.312492    
## ResultSpeed    0.28297    0.06584   4.298 1.74e-05 ***
## ma3            0.59189    0.12213   4.846 1.28e-06 ***
## ma5           -0.70982    0.13854  -5.124 3.07e-07 ***
## ma10           0.71418    0.09174   7.785 7.89e-15 ***
## precip3d     -36.36560    1.61641 -22.498  < 2e-16 ***
## precip5d      45.13598    2.27255  19.861  < 2e-16 ***
## precip10d      4.07897    1.53368   2.660 0.007839 ** 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 15.17 on 7866 degrees of freedom
## Multiple R-squared:  0.1198, Adjusted R-squared:  0.1181 
## F-statistic: 71.37 on 15 and 7866 DF,  p-value: < 2.2e-16

Evaluate linear model for predicting mosquito number

The R^2 of the first model is 0.11, meaning that only 11% of observed mosquito population variation is explained by our weather model. To further evaluate the linear regression model, we can examine the residual errors against predicted numbers in the training data.

print(paste("RMSE score of lm1 on training data: ", round(RMSE(number_train$lmNumMosq, number_train$NumMosquitos), 1)))

## [1] "RMSE score of lm1 on training data:  15.2"

print(paste("RMSE score of lm1 on validation data: ", round(RMSE(number_valid$lmNumMosq, number_valid$NumMosquitos), 1)))

## [1] "RMSE score of lm1 on validation data:  15.3"

ggplot(data = number_valid, aes(x=lmNumMosq, y=(NumMosquitos - lmNumMosq))) + 
  geom_point(alpha = 0.05) + 
  ggtitle("Residual plot for estimating Mosquito number using linear model on weather data") +
  xlab("Predicted number of mosquitoes in training set") + 
  ylab("Residual error (Actual - Predicted)") + 
  stat_smooth(method=lm)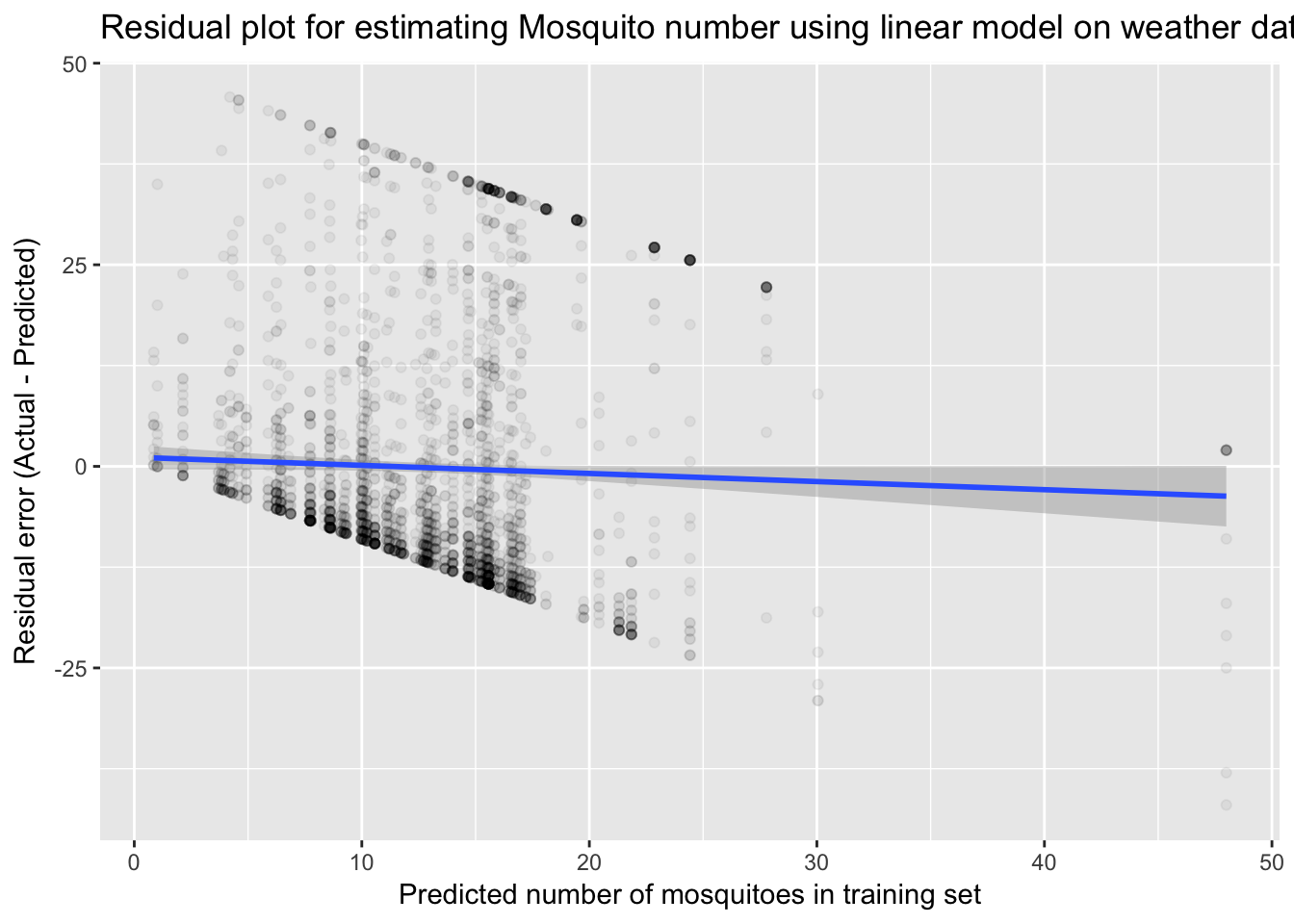

The residual plot appears to show bias in overestimating mosquitoes at the low end and underestimating at the high end. However, the trend shows that this is indeed zero. The odd shape is due to the fact that our actual values are bounded from 1-50. Let’s now include historical averages for each week in the year. We can also remove some variables that were not significantly informative in the previous model.

lm_variables2 <- c("WeekAvgMos",
                  "Tavg",
                  "Tmin",
                  "WetBulb",
                  "ResultSpeed",
                  "ma5",
                  "ma10",
                  "precip5d")

lm_variables2 <- paste(lm_variables2, collapse = "+")
fmla2 <- as.formula(paste("NumMosquitos", lm_variables2, sep = "~"))

lm2 <- train(form = fmla2, 
             data = number_train, 
             method = "lm")

number_train$lm2NumMosq <- predict(lm2, newdata = number_train)

number_valid$lm2NumMosq <- predict(lm2, newdata = number_valid)

train$lm2NumMosq <- predict(lm2, newdata = train)

test$lm2NumMosq <- predict(lm2, newdata = test)

summary(lm2)

## 
## Call:
## lm(formula = .outcome ~ ., data = dat)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -17.387 -11.454  -5.746   4.716  47.520 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) -14.27825    3.09657  -4.611 4.07e-06 ***
## WeekAvgMos    0.83001    0.06830  12.153  < 2e-16 ***
## Tavg          0.20815    0.08394   2.480   0.0132 *  
## Tmin          0.06859    0.07050   0.973   0.3306    
## WetBulb      -0.05817    0.08327  -0.699   0.4848    
## ResultSpeed   0.08779    0.06540   1.342   0.1795    
## ma5           0.02772    0.08301   0.334   0.7384    
## ma10         -0.02540    0.09034  -0.281   0.7786    
## precip5d      0.87161    0.67629   1.289   0.1975    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 15.63 on 7873 degrees of freedom
## Multiple R-squared:  0.06467,    Adjusted R-squared:  0.06372 
## F-statistic: 68.04 on 8 and 7873 DF,  p-value: < 2.2e-16

print(paste("RMSE score of lm2 on training data: ", round(RMSE(number_train$lm2NumMosq, number_train$NumMosquitos), 1)))

## [1] "RMSE score of lm2 on training data:  15.6"

print(paste("RMSE score of lm2 on validation data: ", round(RMSE(number_valid$lm2NumMosq, number_valid$NumMosquitos), 1)))

## [1] "RMSE score of lm2 on validation data:  15.6"

This results in an even lower R^2 value of 0.06 and a higher RMSE error score. Since these values are against the training data this could mean that the first model is overfitting the training set. This is entirely possible since it included a larger number of input variables. The best way to test this is testing and evaluating against our hold-out data. The hold-out RMSE for lm1 was 783.6 and for lm2 was 799.1, so here again we are better with the first model.

A further look at mosquito number distribution

To get a better estimate of mosquito counts, I next wanted to go back and examine the distribution of the Mosquito counts a bit further. The total number with each observation is capped between 1 and 50 mosquitoes. Since there are several rows of data for each trap/date combination when one trap has the full 50 mosquitos, this is likely how the mosquitos are split up for testing. Mosquitoes are collected in the traps and split up into groups with no more than 50 mosquitos, recorded for Species and then tested for WNV. To help correct for this, I added up all of the multiple observations per trap to This distribution is not at all near normal or gaussian, as you can see by the histograms below, and instead resembles a Poisson distribution with no zeros and a cap at 50. Compare the QQplots of Normal and Poisson (\(\lambda = 12.8\)) distributions against log2 transformed number of mosquitos.

Mosq_number <- train %>% group_by(Trap, Date) %>% summarise(Mosq_count = sum(NumMosquitos), nrows = n())

poissonlist <- rpois(1000, 12.8)
poissonlist[poissonlist == 0] <- 1

par(mfcol = c(2,2))
hist(Mosq_number$Mosq_count, col = "lightblue", main = "Histogram mosquito number")
qqnorm(log2(Mosq_number$Mosq_count), main = "QQPlot Normal distribution")
hist(log2(Mosq_number$Mosq_count), col = "lightblue", main = "Histogram log2 mosquito number")
qqplot(poissonlist, log2(train$Mosq_count), main = "QQPlot Poisson with 0 removed")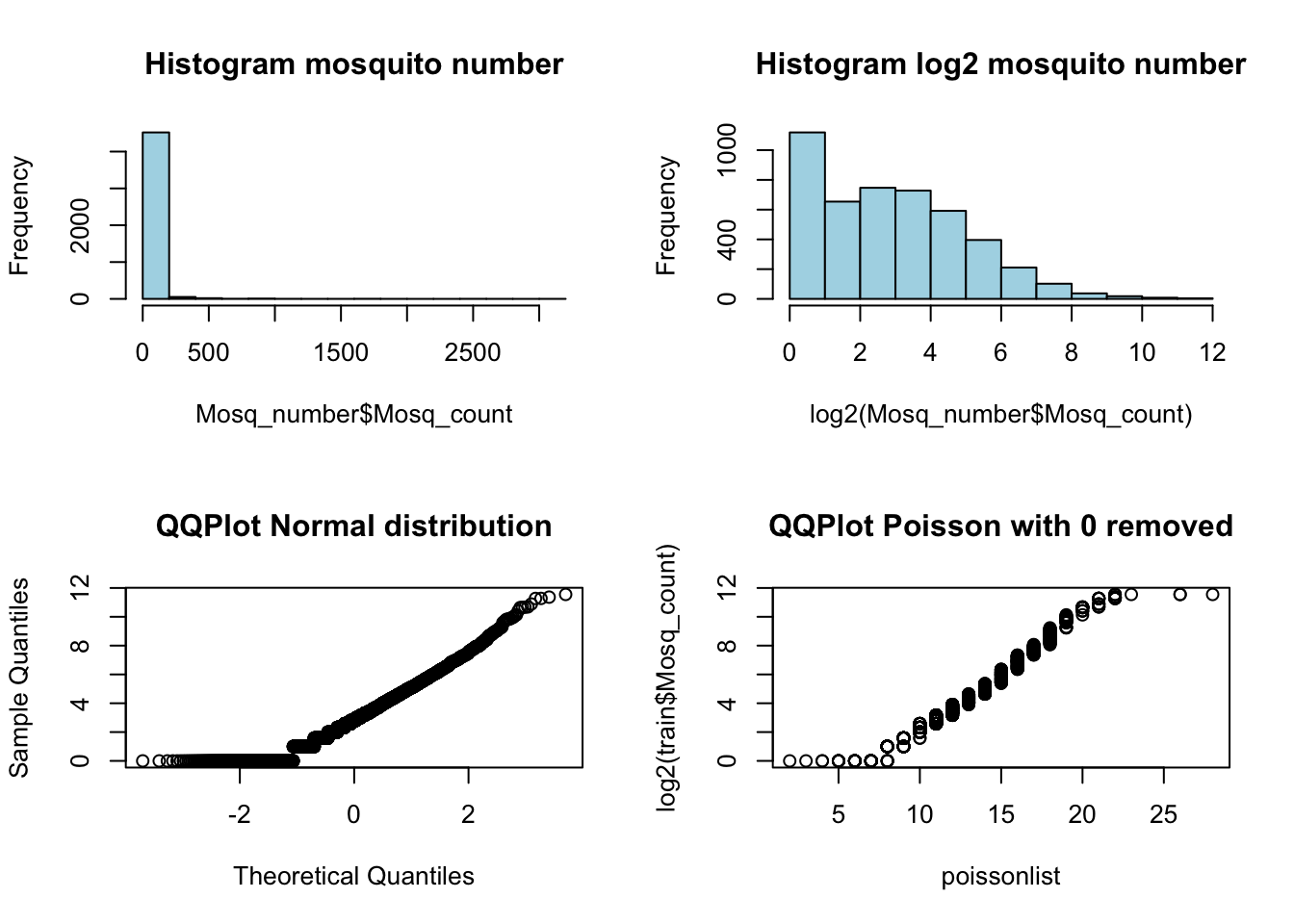

par(mfcol = c(1,1))

Modeling: Poisson Regression

poisson <- train(form = fmla, 
             data = number_train, 
             method = "glm",
             family = "poisson")

number_train$poissonNumMosq <- predict(poisson, newdata = number_train)
number_valid$poissonNumMosq <- predict(poisson, newdata = number_valid)

train$poissonNumMosq <- predict(poisson, newdata = train)

test$poissonNumMosq <- predict(poisson, newdata = test)

summary(poisson)

## 
## Call:
## NULL
## 
## Deviance Residuals: 
##    Min      1Q  Median      3Q     Max  
## -9.323  -3.574  -1.959   1.322  12.737  
## 
## Coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -1.662e+01  5.705e-01 -29.137  < 2e-16 ***
## Tmax         1.039e-01  7.372e-03  14.088  < 2e-16 ***
## Tmin         1.418e-01  7.404e-03  19.152  < 2e-16 ***
## Tavg        -2.513e-01  1.450e-02 -17.324  < 2e-16 ***
## DewPoint    -6.724e-02  2.798e-03 -24.034  < 2e-16 ***
## WetBulb      8.645e-02  4.299e-03  20.110  < 2e-16 ***
## Sunrise      8.011e-03  3.140e-04  25.511  < 2e-16 ***
## Sunset       5.778e-03  2.411e-04  23.965  < 2e-16 ***
## PrecipTotal -1.146e-01  1.154e-02  -9.932  < 2e-16 ***
## ResultSpeed  3.080e-02  1.214e-03  25.365  < 2e-16 ***
## ma3          4.648e-02  2.304e-03  20.172  < 2e-16 ***
## ma5         -6.352e-02  2.612e-03 -24.320  < 2e-16 ***
## ma10         6.718e-02  1.763e-03  38.097  < 2e-16 ***
## precip3d    -1.848e+00  2.142e-02 -86.233  < 2e-16 ***
## precip5d     2.198e+00  3.065e-02  71.714  < 2e-16 ***
## precip10d    1.973e-01  2.546e-02   7.750 9.21e-15 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Dispersion parameter for poisson family taken to be 1)
## 
##     Null deviance: 134193  on 7881  degrees of freedom
## Residual deviance: 116462  on 7866  degrees of freedom
## AIC: 145001
## 
## Number of Fisher Scoring iterations: 5

print(paste("RMSE score of Poisson regression on validation set: ", round(RMSE(number_valid$poissonNumMosq, number_valid$NumMosquitos), 1)))

## [1] "RMSE score of Poisson regression on validation set:  15.2"

This is slightly better than standard linear regression, with an RMSE of 778.5. I will this estimate for the number of mosquitos in the final prediction for WNV in the test set.

Examining the effect of geography and location

In addition to mosquito population size and weather variables, there is likely to be an effect based on a trap’s geographic location. Next, I wanted to visually examine the relationship between geography and West Nile presence. In other words, I wanted to make some cool maps! First I created a map of Wnv incidents as a density plot. Here, the density is derived from the overall positive count for each trap.

library(ggmap)
chicago <- get_map("Chicago")

## Map from URL : http://maps.googleapis.com/maps/api/staticmap?center=Chicago&zoom=10&size=640x640&scale=2&maptype=terrain&language=en-EN&sensor=false

## Information from URL : http://maps.googleapis.com/maps/api/geocode/json?address=Chicago&sensor=false

wnpositive <- filter(train, WnvPresent == TRUE)
load("west-nile/traps.RData")

ggmap(chicago) + geom_density2d(data = wnpositive, aes(x = Longitude, y = Latitude), size = 0.3) + 
  stat_density2d(data = wnpositive, aes(x = Longitude, y = Latitude, fill = ..level.., alpha = ..level..), size = 0.01, bins = 16, geom = "polygon") + 
  scale_fill_gradient(name="Number of WNV+", low = "green", high = "red") + 
  scale_alpha(range = c(0, 0.3), guide = FALSE) + 
  ggtitle("Heat map of West Nile Virus positive traps") + 
  xlab("Longitude") + ylab("Latitude") +
  geom_point(data = traps, aes(x = Longitude, y = Latitude), shape = 4)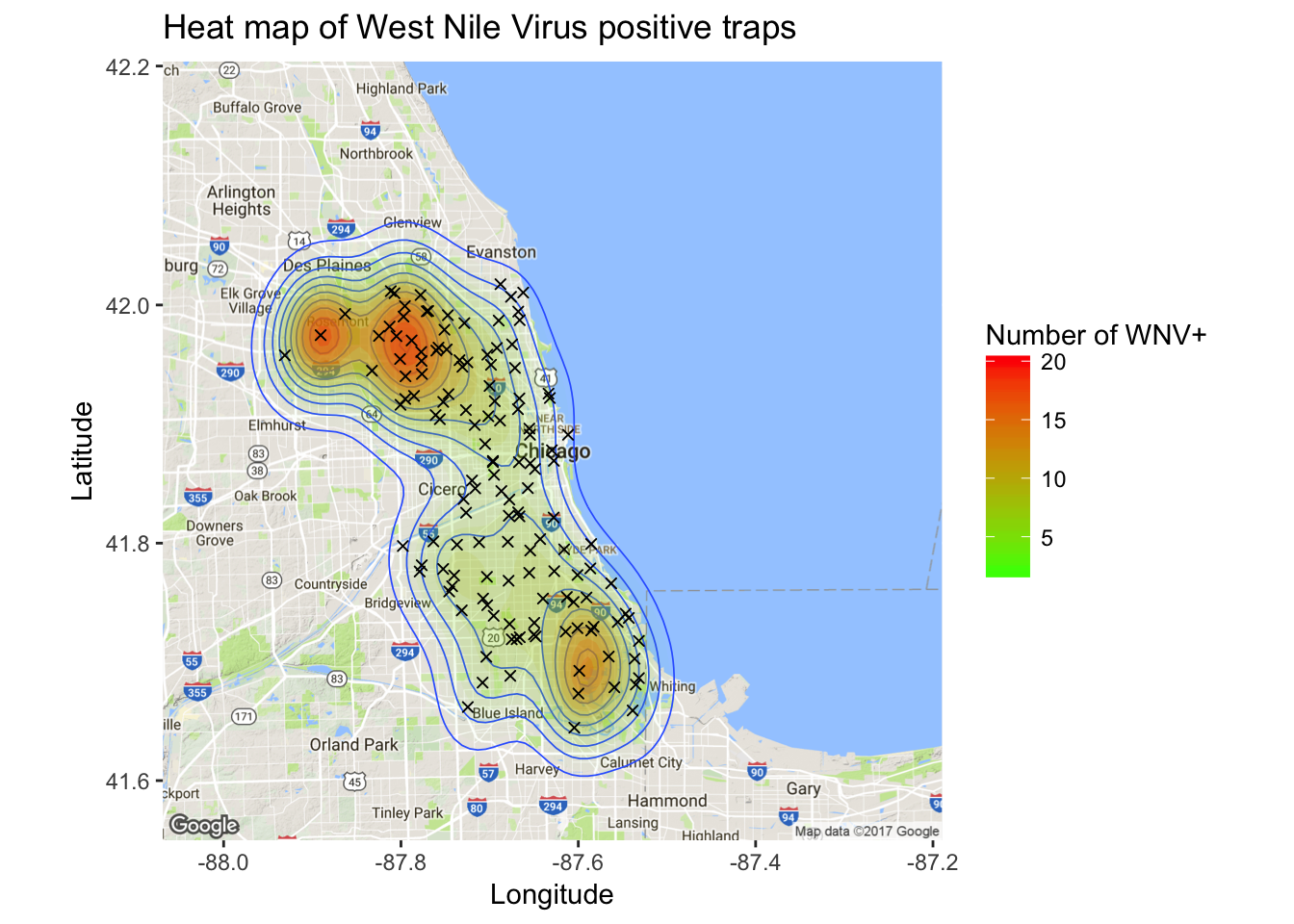

It’s clear from the density map that there are hotspot traps where West Nile is more common than others, and this appears to influence nearby traps.

Now that we have a good 2-dimensional view of the occurence of WNV, I next wanted to get a sense of how this pattern of West Nile Virus changed over time in relation to the geography. I did this by creating an animated version of this map using a new R package called gganimate. I chose to remove the background map of Chicago to get a clearer visual of positive vs negative cases. This animation uses the new gganimate package.

library(gganimate)
library(animation)

byyearweek <- group_by(train, Year, Week) %>% summarize(weekly_avg_mosq = mean(NumMosquitos))
train$timepoint <- ((train$Year - 2007) + (train$Week / 52)) * 52

map_mosq <- ggplot(train, aes(x=Longitude, y=Latitude, 
                                  size=NumMosquitos, 
                                  color=WnvPresent,
                                  frame=timepoint)) + geom_point(alpha = .5) + 
                                  ggtitle("Animated map of mosquitos and \npresence of West Nile Virus in Chicago \n")

animated_map_mosq <- gganimate(map_mosq, interval=0.5)
animated_map_mosq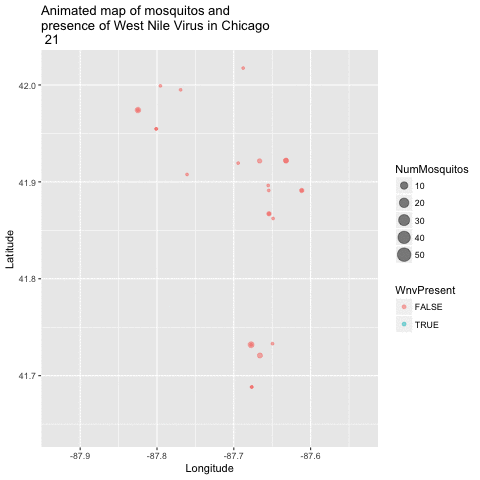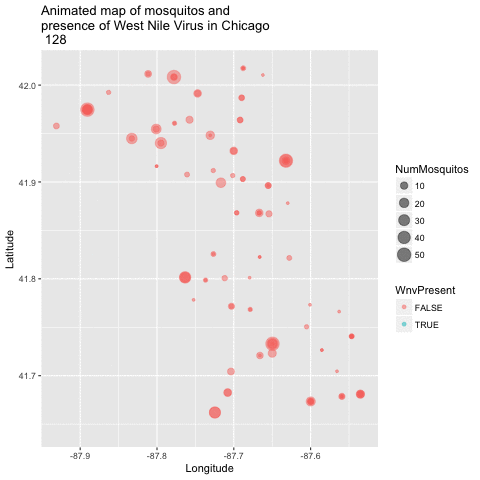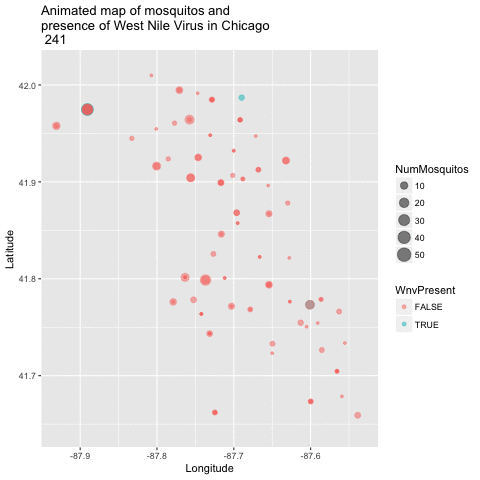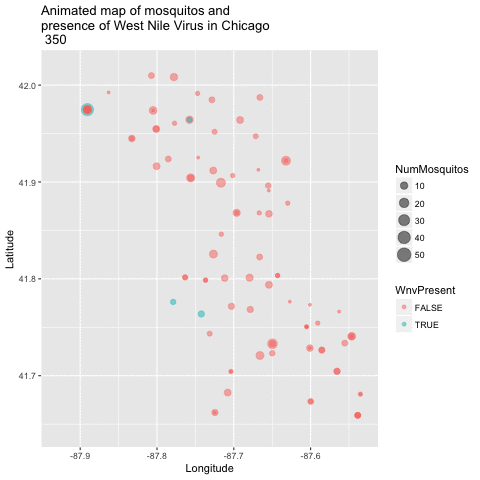

Mosquito map

There are various ways to incorporate geography into a predictive model. I could incorporate the trap id in the model or I could incorporate the longitude and latitude for very high precision. The longitude/latitude method would require a decision tree or other model that allows for breaking up or clustering the locations in some non-linear way.

Instead, I am choosing to group the traps into clusters and include the cluster as a modeling parameter. The reasoning for this is that suspect that the true risk based on geography has a much lower actual precision than our ability to define latitude or longitude.

Data preparation: Clustering traps according to location and WNV presence

To create clusters of traps I want to incorporate not only geographical information, but WNV rate as well. This will help to create breaks in my clusters that are informative for predicting future WNV rate. The code for clustering is found in the “04_geo_cluster.R” script.

load("west-nile/train_geo.RData")
load("west-nile/test_geo.RData")
load("west-nile/trap_geo_hot.RData")

ggplot(trap_geo_hot, aes(Longitude, Latitude, color = geo.hot.cl)) + geom_point()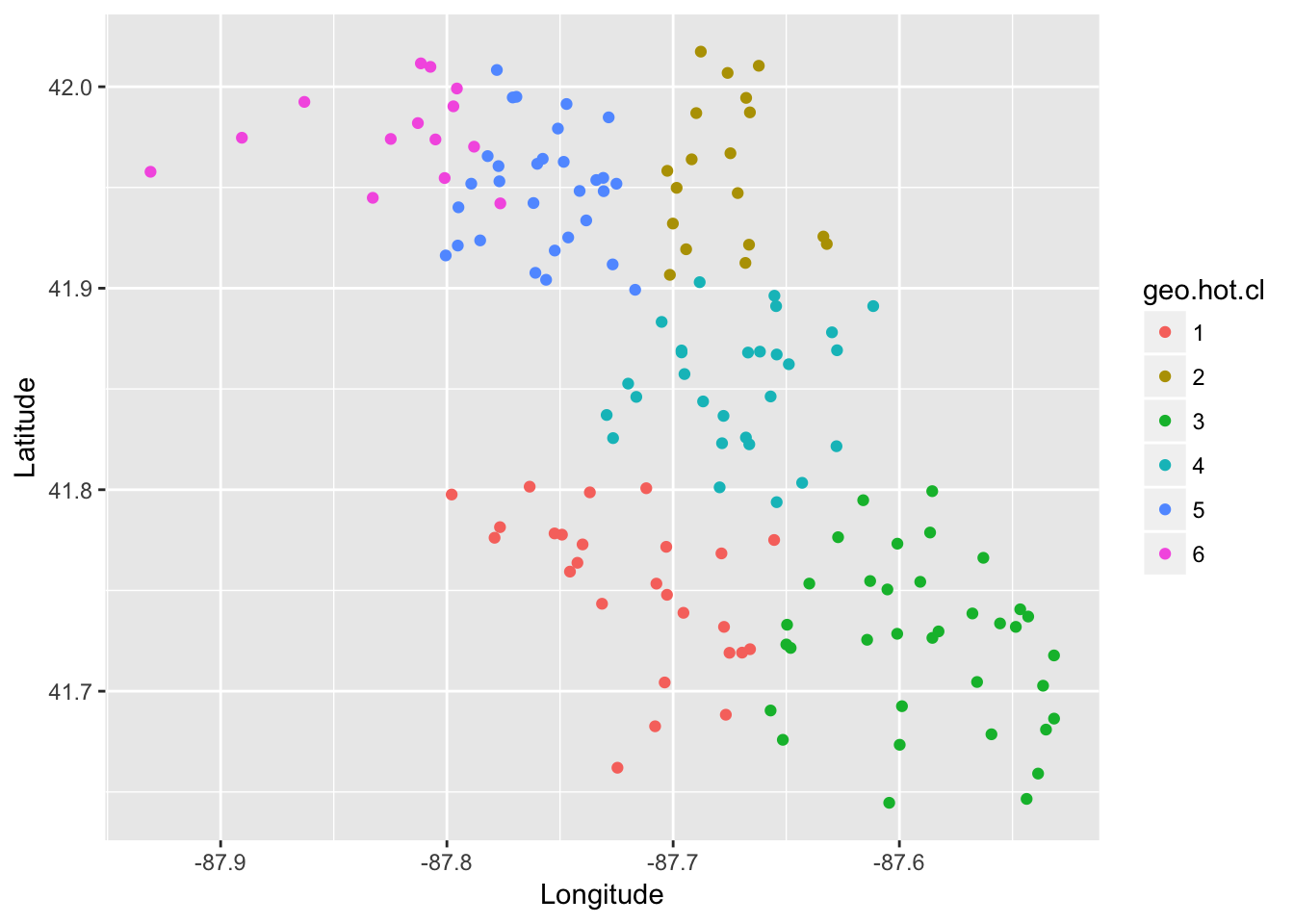

ggmap(chicago) + geom_density2d(data = wnpositive, aes(x = Longitude, y = Latitude), size = 0.3) + 
  stat_density2d(data = wnpositive, aes(x = Longitude, y = Latitude, fill = ..level.., alpha = ..level..), size = 0.01, 
    bins = 16, geom = "polygon") + 
  scale_fill_gradient(name="Number of WNV+", low = "green", high = "red") + 
  scale_alpha(range = c(0, 0.3), guide = FALSE) + 
  ggtitle("Heat map of West Nile Virus positive traps") + 
  xlab("Longitude") + ylab("Latitude") +
  geom_point(data = trap_geo_hot, aes(x = Longitude, y = Latitude, shape = geo.hot.cl)) + scale_shape_discrete(name = "Trap Cluster")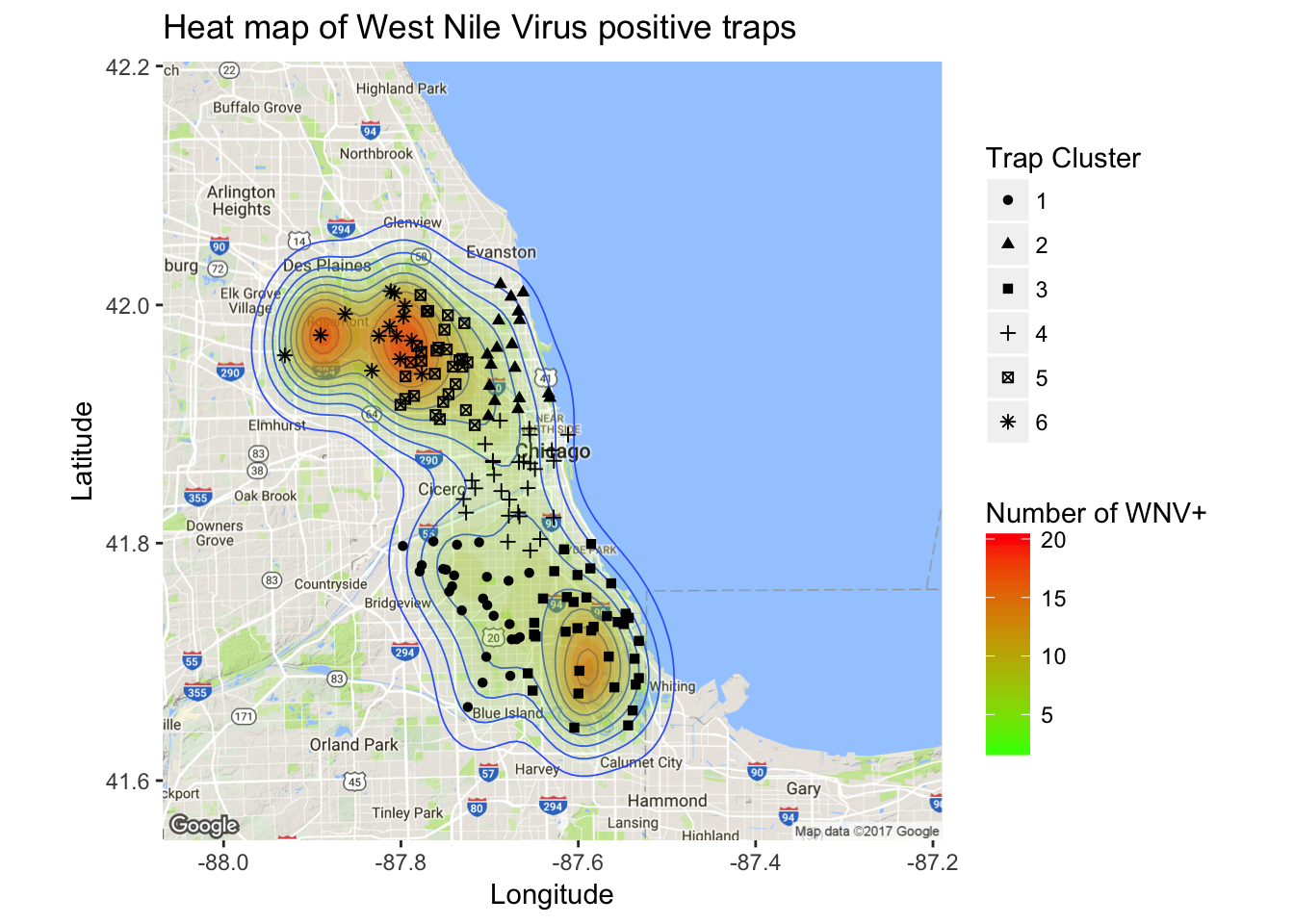

Now that I have some geographical clusters for each trap and a good handle on predicting mosquito number, I can use those as input variables for the ultimate target, WNV probability. I will be comparing several different models for my next post.

Bibliography